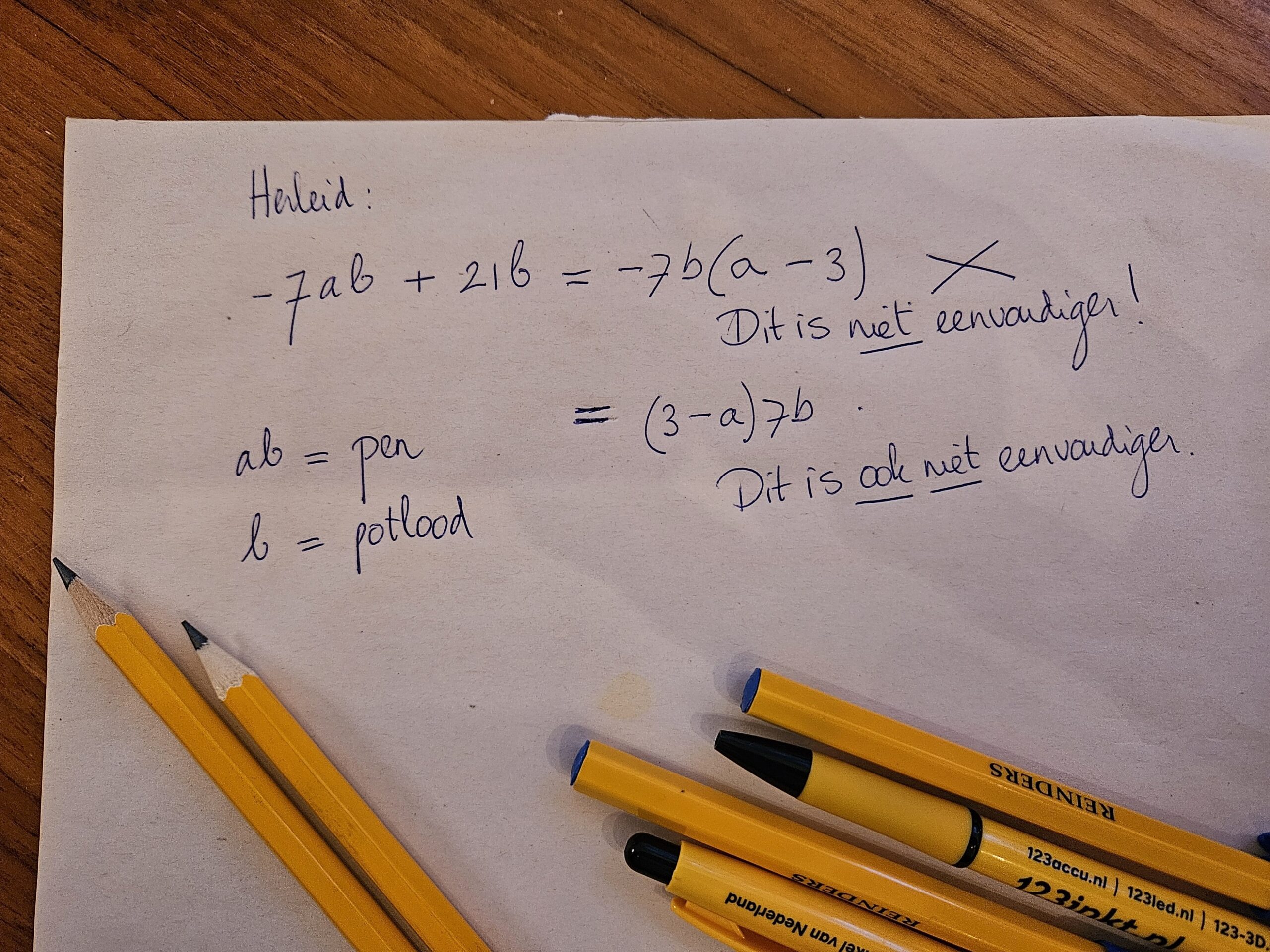Ik vind (minstens) twee dingen erg leuk aan brugklassers. Allereerst hebben ze nog drive om elleke opgave goed te doen. En verder, ikzelf word nog regelmatig uitgedaagd om dat wat onderhand superrr-logisch is, begrijpelijk uit te leggen.
Wat betekent “herleiden”?, vraag ik mijn brugger als we beginnen met de les. Dat is hij even vergeten, maar … dat is hetzelfde als vereenvoudigen. Tja, wanneer noem je de ene wiskunde eenvoudiger dan de andere? Het is al zo lastig! We praten zo even over ‘gelijknamige termen’, minimaliseren van haakjes en “min-keer-min-is-plus”.
Ik denk dat hij het begrijpt en de eerste herleiding gaat goed: -2a – 3*2a = -2a-6a. Maar dan, als ik vraag of het nog eenvoudiger kan: “Natuurlijk mevrouw, al die minnetjes zijn maar bar ingewikkeld, dus hatsjiekidee!”: -2a-6a = 12a. Verrassend.
Na een uitleg over het verschil tussen optellen en vermenigvuldigen, komt de volgende uitdaging: 4x*3y + 2x*6z = 12xy + 12xz. So far, so good. En dan weer een oplossing uit onverwachte en ijverige, doch foutieve hoek:
12xy + 12xz = 24xyz!
Oké, die uitleg van net kan beter. Ik pak er een stel potloden en pennen bij. Stel je voor dat y een potlood is, z een pen en x een likje rode verf. Dan heb jij zonet rode potloden en rode pennen over één kam geschoren en daarmee de unieke identiteit van een stuk schrijfwaar ontnomen. We kijken elkaar aan en moeten hard lachen. “Goeie genade. Dit vergeet ik nooit meer”, zegt mijn brugger.